- épicycloïde
-
épicycloïde [ episiklɔid ] n. f.• 1687; de épicycle, d'apr. cycloïde♦ Géom. Courbe engendrée par un point d'un cercle qui roule sans glisser sur un autre cercle (⇒ cycloïde). — Adj. ÉPICYCLOÏDAL, ALE, AUX , (1741) .
● épicycloïde nom féminin Courbe plane engendrée par un point fixé d'un cercle (C′) roulant sans glisser à l'extérieur d'un cercle fixe (C), le rapport des rayons R de (C) et r de (C′) étant un nombre rationnel. (Pour R = r, on a la cardioïde, pour R = 2 r, la néphroïde.)épicycloïden. f. GEOM Courbe décrite par un point d'un cercle qui roule sans glisser sur un autre cercle, à l'extérieur de celui-ci. (V. hypocycloïde.)⇒ÉPICYCLOÏDE, subst. fém.GÉOM. Courbe décrite par le point d'un cercle qui roule sans glisser sur un autre cercle (cf. CHAMPLY, Nouv. encyclop. prat., t. 19, 1927, p. 159). Cf. hypocycloïde.Prononc. et Orth. :[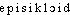 ]. Ds Ac. 1762-1932. Étymol. et Hist. 1687 (Ph. de La Hire ds Hist. de l'Acad. des sciences, II, 55 ds DG). Composé de cycle; préf. épi-; suff. -oïde sur le modèle de cycloïde.DÉR. Épicycloïdal, ale, aux, adj. a) Géom. Relatif à une épicycloïde. On peut l'observer [la mutation] sur la toupie; en produisant une perturbation dans sa précession, on amène l'extrémité à décrire, au lieu d'un cercle, une courbe épicycloïdale (LEDIEU, CADIAT, Nouv. matér. nav., 1890, p. 14). b) Automob., mécan. Engrenage épicycloïdal. Où la roue centrale autour de laquelle tourne le pivot est fixe. Engrenage épicycloïdal différentiel. Où la roue a sa rotation propre (cf. BASSERMANN-JORDAN, Montres, horl. et pend., 1964, p. 187). Boîte de vitesse à train épicycloïdal. Qui réunit les deux moitiés d'essieu d'un véhicule (cf. CHAPELAIN, Techn. automob., 1956, p. 90). — [
]. Ds Ac. 1762-1932. Étymol. et Hist. 1687 (Ph. de La Hire ds Hist. de l'Acad. des sciences, II, 55 ds DG). Composé de cycle; préf. épi-; suff. -oïde sur le modèle de cycloïde.DÉR. Épicycloïdal, ale, aux, adj. a) Géom. Relatif à une épicycloïde. On peut l'observer [la mutation] sur la toupie; en produisant une perturbation dans sa précession, on amène l'extrémité à décrire, au lieu d'un cercle, une courbe épicycloïdale (LEDIEU, CADIAT, Nouv. matér. nav., 1890, p. 14). b) Automob., mécan. Engrenage épicycloïdal. Où la roue centrale autour de laquelle tourne le pivot est fixe. Engrenage épicycloïdal différentiel. Où la roue a sa rotation propre (cf. BASSERMANN-JORDAN, Montres, horl. et pend., 1964, p. 187). Boîte de vitesse à train épicycloïdal. Qui réunit les deux moitiés d'essieu d'un véhicule (cf. CHAPELAIN, Techn. automob., 1956, p. 90). — [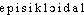 ]. — 1re attest. 1845 (BESCH. Suppl.); de épicycloïde, suff. -al.épicycloïde [episiklɔid] n. f.❖♦ Géom., techn. Courbe engendrée par un point d'un cercle (dit générateur) qui roule sans glisser à l'extérieur d'un autre cercle (dit directeur) [opposé à hypocycloïde]. ⇒ Cycloïdal, cycloïde. || Épicycloïde plane, sphérique.0 La lune décrit un orbe presque circulaire autour de la terre; mais vue du soleil, elle paraît décrire une suite d'épicycloïdes dont les centres sont sur la circonférence de l'orbe terrestre; pareillement la terre décrit une suite d'épicycloïdes dont les centres sont sur la courbe que le soleil décrit autour du centre de gravité du groupe d'étoiles dont il fait partie; enfin le soleil décrit lui-même une suite d'épicycloïdes dont les centres sont sur la courbe décrite par le centre de gravité de ce groupe autour de celui de l'univers (…)Laplace, Exposition du système du monde, V, 6.❖DÉR. Épicycloïdal.
]. — 1re attest. 1845 (BESCH. Suppl.); de épicycloïde, suff. -al.épicycloïde [episiklɔid] n. f.❖♦ Géom., techn. Courbe engendrée par un point d'un cercle (dit générateur) qui roule sans glisser à l'extérieur d'un autre cercle (dit directeur) [opposé à hypocycloïde]. ⇒ Cycloïdal, cycloïde. || Épicycloïde plane, sphérique.0 La lune décrit un orbe presque circulaire autour de la terre; mais vue du soleil, elle paraît décrire une suite d'épicycloïdes dont les centres sont sur la circonférence de l'orbe terrestre; pareillement la terre décrit une suite d'épicycloïdes dont les centres sont sur la courbe que le soleil décrit autour du centre de gravité du groupe d'étoiles dont il fait partie; enfin le soleil décrit lui-même une suite d'épicycloïdes dont les centres sont sur la courbe décrite par le centre de gravité de ce groupe autour de celui de l'univers (…)Laplace, Exposition du système du monde, V, 6.❖DÉR. Épicycloïdal.
Encyclopédie Universelle. 2012.
